WP4: System Identification for Robust Control
Task 4.1: Nonlinear system identification with uncertainty quantification
While aeroelastic models are vital in the design stage of wind turbines to predict fatigue and extreme loads, power production and evaluate possible control systems, it is inevitable that many factors contribute to uncertainty or errors in the prediction of dynamic modes and time constants. Among those are: differences between expected and actual material properties; differences in manufacturing; differences in soil or foundation characteristics and modelling assumptions. These uncertainties mainly result in rather suboptimal controllers and conservative safety factors. System identification may aid in understanding the true underlying dynamics and as a consequence may be a key enabler for improvements to the design of controllers and the amount of conservatism of the different safety factors.
There are two main open fundamental issues which further hamper the application of system identification for the wind community. These two issue will be introduced below and are the main topics of this part of the proposal.
Task 4.1.1: Uncertainty quantification
System identification will reveal the underlying true dynamics of the wind turbine. However, since these techniques depend on a number of priors the estimated model will have a certain uncertainty. Descriptions of these uncertainties are hard to obtain for state-of-the-art wind turbine identification methods, which are based on the so-called subspace paradigm. While one could derive first order variance results for subspace methods, just as is typically done for optimization based methods, it is unlikely that results will be reliable. It seems that development of tailored Monte Carlo methods and bootstrapping techniques could be much more useful, such that based on a limited number of independent identification experiments a good characterisation of uncertainties can be found.
The objective of this work package is to develop an algorithm using randomized algorithms (such as bootstrapping) to add an uncertainty quantification to the identified model. One might think of an estimate of the structural damping of the support structure with uncertainty description which could potentially lower the safety factors of the support structure design. Moreover, the identified models combined with their uncertainty set will be used for fault detection and fault tolerant control (WP 2.2).
Task 4.1.2: Nonlinear system identification
Moreover, wind turbines are nonlinear systems current practice is to identify models in several operating points. However, since wind turbines operate in a continuously changing wind field it can be particularly difficult to maintain a reasonably steady operating point. This makes it hard, if not impossible, to obtain suitable data records for LTI system identification, since large wind speed variations cause the linearity assumptions to be violated. The consequence is that one can only identify a “mean” model which describes the experimental data in the best way. If one could explicitly model the dominant nonlinear effects, one could use an arbitrary sequence of data obtained from the turbine, in which the wind speed varies. The current state-of-the-art is to identify so-called Hammerstein (or interpolation) models which combine the static nonlinear behaviour with an LTI dynamic part.
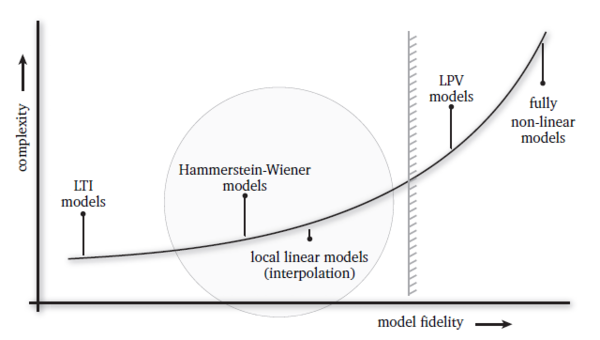
It was also shown that this model structure doesn’t capture all the dominant dynamics of a wind turbine. Linear Parameter Varying (LPV) have a higher fidelity level and efficient controller synthesis techniques are available. However, for system identification a computational traceable algorithm is still lacking.
The objective of the work package is to develop an LPV identification scheme that beats the curse-of-dimensionality in state-of-the-art techniques by using tensor algebra. This will result in efficient data use and reduced uncertainty sets. Moreover, the framework developed in WP 4.1.1. will be extended to this model class.
Background:
Conventionally, wind turbine control algorithms are developed based on physical modelling of the control-relevant dynamics. Although this approach is intuitive and leads to simple (yet practical) control structures, the inherent uncertainty in the physical parameters involved in such “first-principles” models requires the use of conservative stability margins during the control design, associated with decreased overall controller performance. A noticeable improvement of the performance of the wind turbine controllers is expected to be achievable when more accurate (i.e. less uncertain) models are available. In WP4.1 system identification algorithms are developed that reduce the model uncertainties. The resulting less-uncertain models will be used in this WP4.2 to optimize the parameters of the wind turbine controller.
In contrast to above off-line controller optimization, system identification can also be used continuously in an online setting, providing up-to-date information about important wind turbine parameters (e.g. frequencies of tower, drive train). Adapting the controller parameters to the changing turbine parameters will ensure constantly optimized and stable wind turbine controller. Such adaptive control schemes are particularly relevant offshore where the environmental conditions (e.g. water depth changes due to tides and/or scour, ice formation, etc.) can give rise to significant changes of the system parameters, which degrade the performance of the wind turbine controller.
Finally, this WP4.2 will also bridge the gap between existing condition monitoring (CM) schemes and the wind turbine control algorithms by developing a CM-driven controller reconfiguration (CR). In contrast to the “standard fault-tolerant control” approach, where action is taken after a failure has been detected, the CR approach pursued here aims at preventing overall failure (and, hence, shutdown). A good example here is the pitch mechanism, which due to its high failure rate is often one of the most important source of downtime. By detecting degraded performance (due to, e.g. increased friction, wear in the teeth, etc), an number of active vibration control loops can be deactivated and the turbine can be operated at reduced power to significantly relieve the loading on the pitch mechanism. To this end, CM will be used to constantly diagnose the condition of important subcomponents, and once a deviation from the normal operation condition is detected, the wind turbine controller will be reconfigured in order to reduce the loading of this component as much as possible, while at the same time keeping the wind turbine in operation. This delays the failure of the component, giving more time for performing planned maintenance.
The activities within WP4.2 are organized in two main tasks:
Task 4.2.1: Controller re-optimization based on identified models
Starting point here are the reduced-uncertainty models, derived using the methods of WP2.1, as well as other existing methods for (recursive) online system identification.
Task 4.2.1.1 Offline controller optimization based on identified models with reduced uncertainties
Task 4.2.1.2 Online adaptive control for changing turbine parameters
Task 4.2.2: Controller reconfiguration for degraded wind turbine components
The starting point here is the availability of condition monitoring scheme providing information components with degraded performance (pitch mechanism, drive-train).
Task 4.3: Evaluation of integral impact at system level of technology improvements from WP1, WP2, WP3, and WP4
This is an integrating work package where the integral impact on cost of energy is determined of the technology that has been developed in the other work packages.
Return to Work Packages